세타 표기법(Theta-Notation)
세타 표기는 상한과 하한을 모두 알고 있을 때 사용하는 표기법이다.
조건식은 다음과 같다.
0 ≤ c1g(n) ≤ f(n) ≤ c2g(n)
f(n)을 기준으로 f(n)을 표현하고자 하는 대표값 g(n)을 놓고 보았을 때, g(n)에 어떤 상수를 곱하고 다른 어떤 상수를 곱한 것이 있을 때, f(n)은 반드시 샌드위치처럼 끼어 있어야 한다.
해당 조건식에서 상수는 c1, c2 이다.

n이 n0보다 높은 시점에서 f(n)은 항상 c1g(n)보다는 높고 c2g(n)보다는 작다.
이를 'f(n)은 g(n)과 같은 증가속도를 가진다.' 라고 하며 f(n)은 theta of g(n)에 속한다 라고 한다.
g(n)은 f(n)의 점근적 상한 및 하한(asymptotically tight bound)이다.
n이 점근적으로 커질 때, g(n)이 f(n)을 tight하게 위, 아래로 bound한다.
만약 f(n)이 n의 k승을 포함하고 있는, n의 k승이 차수가 가장 높은 다항식이라면 이 f(n)은 항상 theta of n의 k승에 포함된다.
식으로 표현하면 다음과 같다.
f(n) = Θ(nk)
big - O 표기법(O - Notation)
빅O 표기법은 점근적 상한만을 알고 있을 때 사용하는 표기법이다.
조건식은 다음과 같다.
0 ≤ f(n) ≤ cg(n)
세타 표기법에서 위쪽만을 취하고 아래쪽은 제외한 표기법이다.
f(n)이 big - O of g(n)이라는 것은 f(n)은 0보다는 커야 하고 cg(n)보다는 작아야 한다는 것을 의미한다.
이 조건식을 만족하는 상수 c와 n0가 하나라도 존재한다면 f(n)은 big - O of g(n)이다.
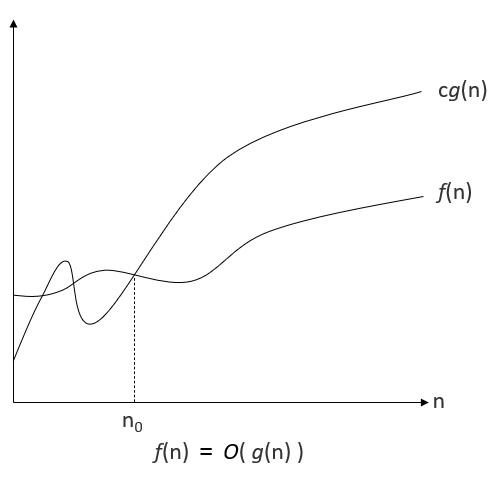
f(n)이 n0를 기점으로 항상 cg(n)보다 작다.
이를 풀어서 설명하면 'f(n)은 절대 cg(n)을 넘어가지 않는다.' 라고 얘기할 수 있으며 이는 '최악의 경우(worst case)에도 이 알고리즘은 cg(n)을 넘어가지 않는다.' 라고 할 수 있다.
때문에 알고리즘의 worst running time을 얘기할 때 유용하다.
g(n)을 f(n)의 점근적 상한(asymptotically upper bound)이라고 얘기한다.
만약 f(n) = Θ( g(n) )이라면 Θ는 상한과 하한을 둘 다 얘기하기 때문에 f(n) = O( g(n) )이라고 얘기해도 맞는 말이다.
오메가 표기법(Ω - Notation)
오메가 표기법은 big - O 표기법과 마찬가지로 한쪽만 취한다.
하지만 big - O와 다르게 취하는 쪽이 아래쪽이다.
조건식은 다음과 같다.
0 ≤ cg(n) ≤ f(n)
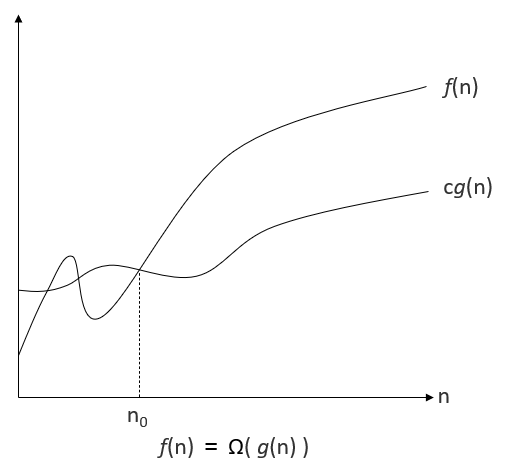
오메가 표기법은 n0를 기점으로 f(n)이 항상 cg(n)보다 크다.
f(n) = Ω( g(n) )이라고 한다면 g(n)을 f(n)의 점근적 하한(asymptotically lower bound)이라고 얘기한다.
이는 '이 알고리즘은 아무리 늦어도 이것 보다는 빠릅니다.' 라는 best running time을 얘기할 때 주로 사용된다.
little - o 표기법(O - Notation)
어떤 함수 f(n)이 little - o의 g(n)이다 라고 하려면 양의 상수 n0가 있어야 한다.
그리고 모든 상수 c에 대해 f(n)이 g(n)보다 작아야 한다.
이렇게 된다면 g(n)은 f(n)의 상한이 된다.
조건식은 다음과 같다.
0 ≤ f(n) < cg(n)
이를 여유있는 상한이라고 하며 주어진 알고리즘이 아무리 나빠도 비교하는 함수보다 좋다는 것을 의미한다.
(not asymptotically tight)
little - omega 표기법(ω - Notation)
f(n) = ω( g(n) )이 되려면 모든 상수 c에 대하여 f(n)이 g(n)보다 큰 식을 만들어야 한다.
조건식은 다음과 같다.
0 ≤ cg(n) < f(n)
little - o 표기와 정확하게 대조되는 표기법이며 여유있는 하한이라고 한다. (not asymptotically tight)
주어진 알고리즘이 아무리 좋아도 비교하는 함수보다 좋지 못하다는 것을 의미한다.
마무리
가장 많이 활용되는 표기법은 세타와 빅오이다.
세타는 tight boundary, 즉 굉장히 정확하게 런타임을 얘기할 수 있다.
빅오는 worst case complexity, 즉 이 알고리즘은 아무리 늦어도 이 시간 안에는 답이 나온다를 설명할 때 사용된다.
실생활을 예로 들자면 이 과목은 아무리 못해도 B는 나와~ 이런 상황에서 빅오를 사용한다.
글에서 설명한 표기법들은 각 알고리즘에 주어진 크기를 기준으로 runtime과 사용 시간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시해 준다.
f (n)과 g(n)을 극한으로 표현할 때 상수가 0보다 크고 무한대보다 작은 어떤 상수에 수렴할 수 있고, 이 상수가 얼마나 클지는 프로그램마다 다르기 때문에 점근분석이 필요하다.
'CS > 알고리즘(Algorithm)' 카테고리의 다른 글
| [Algorithm] 코드 블럭 단위 복잡도 분석 (0) | 2023.03.15 |
|---|---|
| [Algorithm] BFS,DFS 알고리즘 구현(C++) (0) | 2023.02.03 |
| [Algorithm] 그래프 탐색 알고리즘(BFS, DFS) 기본 (0) | 2023.01.29 |
| [Algorithm] 선형검색, 이진검색 알고리즘과 점근분석(Linear&Binary search) (0) | 2023.01.13 |
| [Algorithm] 알고리즘을 배우는 이유 (0) | 2023.01.13 |
![[Algorithm] 점근 표기법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FB6V1W%2FbtrWwLFuZpB%2FBB6bKN45DAiE6VvWRA5910%2Fimg.png)