개요
트리는 노드들의 계층 관계를 표현한 집합체이다.
모양은 침엽수와 같은 나무를 거꾸로 매달아 놓은 것처럼 생겼는데 이제부터 사진들과 함께 알아 볼 것이다.
트리는 종류가 많은데, 해당 글에서는 트리의 정말 기본적인 내용만 다룰 것이다.
규칙
1. 최상위 레벨에 있는 노드는 루트라고 하며 진입 차수가 0이다. 루트 노드는 트리마다 하나밖에 존재하지 않는다.
2. 모든 노드는 0, 또는 n개의 자식 노드를 가진다.
3. 모든 노드는 하나 이상의 부모 노드를 가진다.
4. 트리는 level을 가진다. 가장 꼭대기에 있는 루트 노드는 레벨이 0이며 트리의 루트로부터 특정 vertax까지의 경로 길이로 결정된다.
5. 루트 노드로부터 특정 노드까지의 경로는 반드시 1개만 존재한다.
6. 만약 트리가 루트 뿐이고 자식 노드 없이 텅텅 비어 있다면 해당 트리의 높이는 -1이다.
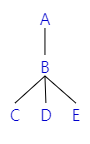
간단한 트리를 하나 만들었다.
여기서 B라는 노드는 C D E 라는 3개의 자식 노드를 가지고 있다.
그러므로 B의 차수는 3이다.
C D E는 같은 높이에 존재하는 노드이다. 이러한 노드를 자매 노드라고 한다. 또한 자식 노드가 없기 때문에 리프 노드이다
C D E는 B라는 부모 노드를 가지며 B의 부모 노드는 A이다.
트리의 레벨은 2이며 레벨별 노드는 다음과 같다.
레벨 0 : A
레벨 1 : B
레벨 2 : C, D, E
레벨을 구하면 트리의 높이도 구할 수 있다.
트리의 높이를 구하는 공식은 [ 가장 높은 레벨 + 1 ] 이다.
해당 공식을 트리 1 사진으로 대입하면 2 + 1이므로 트리의 높이는 3이다.

위의 사진보다 한층 업그레이드 된 트리를 하나 만들었다.
위 트리에서는 빨간색으로 표시한 G까지의 경로를 구할 것이다.
경로는 앞서 말했던 규칙처럼 1개밖에 존재하지 않는다.
G까지의 경로는 A - B - E - G 이며 깊이는 3이다.
컴퓨터에서 트리의 표현

컴퓨터에서 트리는 자식 노드의 개수에 따라 포인터를 가진다.
부모 노드와 자식 노드는 각각 포인터로 연결된다.
트리 3을 컴퓨터에서 표현되는 방식으로 바꿔보도록 하겠다.

컴퓨터에서 트리는 해당 사진과 같이 표현된다.
각각의 자식 노드 개수와 같은 포인터를 가지고 있으며, 포인터들은 자식 노드를 가르키며 서로 연결되어 있는 것을 확인할 수 있다.
'CS > 자료구조(data structure)' 카테고리의 다른 글
| [자료구조] 그래프(Graph)란? (2) | 2023.01.25 |
|---|---|
| [자료구조] 스택과 큐를 이용하여 회문 판별 프로그램 만들기(C++) (0) | 2022.12.30 |
| [자료구조] 큐(Queue)란? (0) | 2022.12.30 |
| [자료구조] 스택(Stack)이란? (1) | 2022.12.27 |
| [자료구조] 연결리스트(Linked List)란? (0) | 2022.12.26 |